출처: http://soen.kr/lecture/library/opengl/opengl-8.htm
29. 행렬
OpenGL은 각종 변환에 행렬을 많이 사용한다. 행렬의 수학적 특성을 잘 이용하면 빠른 속도로 연산을 수행할 수 있다. OpenGL이 변환에 사용하는 행렬은 4*4 크기의 행렬이다. 3차원 공간은 3개의 좌표로 구성되지만 연산의 편의를 위해 한차원 더 높은 4*4 행렬을 사용한다.
메모리에서 4*4 행렬을 표현하는 방법은 여러 가지가 있는데 일단 다음 두 가지를 생각할 수 있다.
GLfloat matrix[4][4]; GLfloat matrix[16];
이차원 배열이 더 직관적이지만 효율은 일차원 배열이 더 좋다. 2차원 배열이라고 해도 어차피 요소 개수가 고정되어 있으므로 1차원으로 표현할 수 있다. 1차원 배열로 고정 크기의 2차원 배열을 표현하는 방법은 원소를 나열하는 순서에 따라 다음 2가지로 나누어진다.
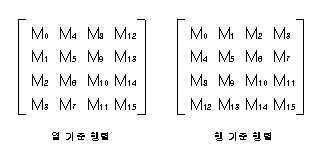
OpenGL은 주로 열 기준 행렬을 사용하는데 열 기준 행렬이 몇 가지 이점이 있기 때문이다. 다음 함수는 배열로부터 열 기준 행열을 읽어들인다. 배열 m은 16개의 요소를 열 기준으로 가지고 있어야 한다.
void glLoadMatrix[f,d](const GLfloat * m);
수학에서는 흔히 행 기준 행렬을 많이 사용한다. OpenGL은 주로 열 기준 행렬을 사용하지만 원한다면 행 기준 행렬도 사용할 수는 있다. 행 기준 행렬로 읽어들일 때는 다음 함수를 사용한다.
void glLoadTransposeMatrix[f, d](const GLfloat * m);
이 함수의 이름에 포함된 Transpose는 전치라는 뜻인데 열 기준 행렬의 전치 행렬이 행 기준 행렬이기 때문이다. 전치라는 것은 대각선을 기준으로 원소를 맞바꾸는 연산이다.
행렬끼리 곱할 때는 다음 함수를 호출한다.
void glMultMatrixf(const GLfloat * m); void glMultTransposeMatrixf(const GLfloat * m);
다음 예제는 주전자를 0.5, 0.5만큼 이동시킨다.
#include <windows.h>
#include <gl/glut.h>
void DoDisplay();
int Action;
int APIENTRY WinMain(HINSTANCE hInstance,HINSTANCE hPrevInstance
,LPSTR lpszCmdParam,int nCmdShow)
{
glutCreateWindow("OpenGL");
glutDisplayFunc(DoDisplay);
glutMainLoop();
return 0;
}
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat trans[16] = {
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0.5, 0.5, 0, 1
};
glMultMatrixf(trans);
glutWireTeapot(0.2);
glPopMatrix();
glFlush();
}
이 행렬은 다음 수식을 정의한다. 열기준 행렬이므로 수학식으로 쓸 때는 전치됨을 주의하자.
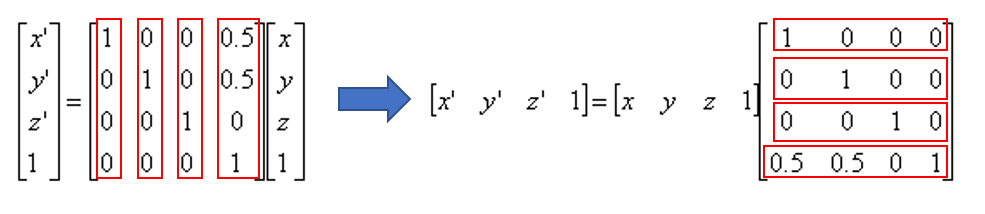
어떤 점 V에 행렬 M을 곱해 V’ 가 생성된다. 수식으로 표현하면 V’ = MV이다. 행렬끼리 곱할 때 앞 행렬의 열 수와 뒤 행렬의 행 수가 같아야 한다. 그래서 M과 V를 곱할 때는 M이 V의 앞에 와 MV가 되어야 한다. VM은 행렬의 규칙상 곱할 수 없는 수식이다.
벡터를 행렬로 표현하는 방법은 행 벡터와 열 벡터 두 가지가 있다. OpenGL은 주로 원소를 세로로 나열하는 열 벡터를 사용한다. 그 이유는 행렬이 열 기준이기 때문이다. 만약 행 벡터를 사용하고 행렬도 행 기준을 사용한다면 위 수식은 V’ = VM이 될 것이다.
위 두 수식은 똑같은 식의 다른 표현일 뿐이다. OpenGL은 주로 전자의 수식을 사용한다. 이 행렬곱에 의해 다음 수식이 생성된다. 행렬식은 단 하나의 수식일 뿐이지만 원소끼리 연산되므로 여러 개의 다항식을 생성해낸다.
x’ = x + 0.5
y’ = y + 0.5
z’ = z
1 = 1
x에 0.5를 더해 x’ 좌표를 정의하고 y에 0.5를 더해 y’ 좌표를 정의하므로 가로, 세로로 0.5만큼 이동하는 것이다. z’는 변화가 없고 마지막 수식은 1 = 1 이라는 더미 식을 만들 뿐이다. 이 행렬식을 대신 생성해 주는 함수가 바로 glTranslatef(0.5, 0.5, 0.0);이다. 이 함수를 호출하면 위 예제의 행렬을 만들어 현재 행렬에 곱함으로써 모든 정점을 이동시키는 효과가 나타난다.
다음은 확대를 해 보자. 앞 예제와 형식은 동일하되 행렬 내부의 원소들이 다를 뿐이다. 원소가 달라지면 다항식의 계수와 더해지는 값이 달라짐으로써 변환 연산도 달라진다.
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat scale[16] = {
2.5, 0, 0, 0,
0, 2.5, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
};
glMultMatrixf(scale);
glutWireTeapot(0.2);
glPopMatrix();
glFlush();
}
이 수식은 glScalef(2.5, 2.5, 1.0)와 동일하다.

이 행렬에 의해 다음 수식이 도출된다. 원래의 x값에 2.5를 곱해 새로운 x를 정의하고 y도 마찬가지로 2.5를 곱한다. 그러므로 가로, 세로로 2.5배 확대되는 것이다.
x’ = 2.5 * x
y’ = 2.5 * y
z’ = z
1 = 1
다음은 z축을 중심으로 45도 회전하는 glRotatef(45.0, 0.0, 0.0, 1.0) 호출문을 행렬로 구현하는 것이다.
#include <math.h>
(...)
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat rotate[16] = {
cos(45.0*3.14/180), sin(45.0*3.14/180), 0, 0,
-sin(45.0*3.14/180), cos(45.0*3.14/180), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
};
glMultMatrixf(rotate);
glutWireTeapot(0.2);
glPopMatrix();
glFlush();
}
회전은 각도의 개념이 들어가므로 삼각함수를 사용하는데 수식의 증명은 생략한다. 수학 함수를 사용하므로 math.h를 인클루드해야 한다.
다음은 확대와 이동을 동시에 수행해 보자. 두 가지 이상의 변환을 복합 변환이라고 하며 둘 이상의 행렬이 순서대로 곱해진다.
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat trans[16] = {
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
-0.2, 0.3, 0, 1
};
glMultMatrixf(trans);
GLfloat scale[16] = {
2.5, 0, 0, 0,
0, 2, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
};
glMultMatrixf(scale);
glutWireTeapot(0.2);
glPopMatrix();
glFlush();
}

곱해지는 행렬이 앞쪽에 붙으며 가해지는 변환의 역순으로 곱해진다. 확대행렬을 S, 이동 행렬을 T라고 할 때 새로운 정점은 다음과 같이 계산된다.
V’ = TSV
수식으로 풀어 보면 다음과 같다.
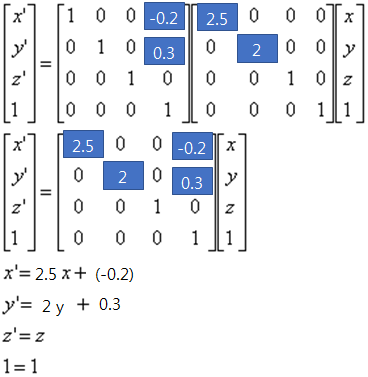
이때 TS는 미리 계산해 둘 수 있다. 행렬은 교환 법칙은 성립하지 않지만 결합 법칙은 성립한다. TS를 미리 곱해 M을 정의하고 V’=MV 연산을 해도 결과는 동일하다. 소스를 다음과 같이 바꾸어도 효과는 동일하다. 앞 예제의 TS를 미리 곱해 하나의 행렬을 정의하고 행렬 곱셈을 한번만 수행한다.
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat transscale[16] = {
2.5, 0, 0, 0,
0, 2, 0, 0,
0, 0, 1, 0,
-0.2, 0.3, 0, 1
};
glMultMatrixf(transscale);
glutWireTeapot(0.2);
glPopMatrix();
glFlush();
}
두 행렬을 미리 곱한 후 벡터에 곱해도 결과는 각각 곱한 것과 동일하다.
3차원 공간의 물체들을 제 위치에 적당한 크기로 배치해 놓고 투영하여 뷰포트에 배치하기까지의 과정을 다음과 같이 수식으로 쓸 수 있다.
V’=POTSRL * V
이 변환을 위해 각 정점마다 이 행렬들을 일일이 곱할 필요가 없다. POTSRL 행렬들을 미리 계산하여 M에 대입해 두면 이후의 변환은 다음 하나의 수식으로 처리된다.
V’=MV
모든 변환 과정을 하나의 행렬 M에 모을 수 있으며 그래서 OpenGL은 모든 변환을 현재 행렬에 누적시킨다. 이것이 가능한 이유는 모든 변환이 행렬의 곱셈으로만 처리되기 때문이다. 행렬의 곱셈은 결합 법칙이 성립됨을 이용하여 미리 계산해 놓고 일관되게 적용한다.
OpenGL은 3차원 그래픽이면서도 4차원의 좌표를 사용함으로써 모든 행렬 연산을 곱셈 하나로 통일하여 행렬 연산을 미리 해 둘 수 있는 것이다.
모든 연산을 곱셈으로 처리하고 미리 계산해 두는 것이 왜 빠른지 예를 들어 보자.
예를 들어 이자율이 10%라면 지급액 = 원금 + 원금 * 0.1 식으로 계산할 수 있지만 덧셈이 들어간다. 또는 이 식을 지급액 = 원금 * 1.1로 곱셈만으로도 표기할 수 있다. 이자율이 10%이고 세율이 2%라 하면 이 식은 다음과 같아진다.
지급액 = 원금 * 1.1 * 0.98
이 수식대로 고객 1000명의 지급액을 계산한다고 할 때 매 고객의 원금마다 1.1 곱하고 0.98을 곱할 필요 없이 1.1과 0.98을 미리 곱한 1.078을 곱하면 된다. 이것이 가능한 이유는 곱셈은 결합 법칙이 성립하기 때문이다.
OpenGL의 행렬에서 중간 변환이 많더라도 성능상의 불이익이 거의 없다. 행렬 곱셈은 사람이 하기에는 복잡한 계산이지만 연산 절차가 단순해서 기계가 하기에는 전혀 어렵지 않으며 초고속으로 처리된다.
다음 예제는 물체를 기울인다.
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
GLfloat sheer[16] = {
1, 0, 0, 0,
0.5, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
};
glMultMatrixf(sheer);
glutWireTeapot(0.5);
glPopMatrix();
glFlush();
}

행렬을 수식으로 바꾸어 계산해 보면 x’ = x + 0.5y가 된다. x 좌표에 y의 절반이 더해지므로 위로 올라갈수록 x 좌표가 더 오른쪽으로 치우치며 원점 아래에서는 오히려 x가 감소한다. 그래서 주전자가 비스듬하게 기울어지는 것이다.
OpenGL이 기울어지는 변환을 함수로 지원하지 않더라도 행렬을 직접 만들어 곱하면 이런 것도 가능하다.
30. 출력 영역의 제한
별다른 제한이 없는 한 모든 출력문은 좌표 공간으로 출력된다. 물론 클리핑이나 뷰포트 변환 단계에서 잘려 나가는 부분이 있지만 그래도 일단은 출력된 후 잘린다. 특정 영역을 아예 처음부터 출력되지 않도록 제한해야 하는 경우가 있는데 이럴 때는 두 가지 방법을 사용할 수 있다
(1) 가위(scissor)를 사용하는 것이다. 가위 기능을 켜 주고 표시할 영역을 알려 주기만 하면 이 영역으로 출력이 제한된다.
glEnable(GL_SCISSOR_TEST);
void glScissor(GLint x, GLint y, GLsizei width, GLsizei height);
사각형 형태로만 제한할 수 있으며 출력 영역을 최소화하는 효과가 있다. 장면의 대부분은 그대로 유지되고 일부만 변한다면 전체 장면을 모두 그릴 필요없이 변하는 부분만 그리면 된다. 무효 영역을 최소화함으로써 출력 속도를 높이는 기법이다.
(2) 스텐실 버퍼로 수행한다. 스텐실 버퍼에 임의의 모양을 그려 두고 이 버퍼와 화면 버퍼를 연산하여 조건에 맞는 부분만 출력할 수 있다. 이 기법을 사용하려면 별도의 스텐실 버퍼를 준비해야 한다. 디스플레이 모드를 초기화할 때 GLUT_STENCIL 플래그를 지정해야 하며 화면을 삭제할 때 스텐실 버퍼도 같이 삭제한다. 깊이 버퍼를 사용하는 방법과 동일하다.
glutInitDisplayMode(GLUT_RGB | GLUT_STENCIL); glClear(GL_COLOR_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
삭제시 스텐실 버퍼에 쓸 값은 glClearStencil 함수로 지정하는데 디폴트가 0이므로 보통은 디폴트를 받아들이면 된다. 스텐실 기능이 켜지면 출력할 때마다 스텐실 테스트를 수행하여 허가된 영역에만 출력을 내 보낸다. 다음 함수로 스텐실 테스트 방법을 지정한다.
void glStencilFunc(GLenum func, GLint ref, GLuint mask);
func는 테스트 함수이다. ref는 비교 대상값이며 mask는 비교전에 대상값과 스텐실값에 & 연산을 취해 특정 비트를 마스크 오프시킨다. 결국 비교 대상은 ref & mask와 스텐실버퍼값 & mask이다. mask의 디폴트는 모든 비트가 1이므로 이 경우 ref와 스텐실 버퍼에 저장된 값을 비교하게 된다. 테스트 함수는 다음과 같다.
GL_NEVER: 항상 실패한다.GL_ALWAYS: 항상 성공한다.GL_LESS: 비교값이 더 작을 때 성공GL_LEQUAL: 비교값이 더 작거나 같을 때 성공GL_GREATER: 비교값이 더 클 때 성공GL_GEQUAL: 비교값이 더 크거나 같을 때 성공GL_EQUAL: 비교값과 스텐실 버퍼값이 같을 때 성공GL_NOTEQUAL: 비교값과 스텐실 버퍼값이 다를 때 성공
스텐실 테스트를 수행한 후 스텐실 버퍼의 값도 변경되는데 다음 함수로 변경 방식을 지정한다. 세가지 경우에 대해 각각 어떤식으로 변경할 것인가를 지정한다.
void glStencilOp(GLenum sfail, GLenum dpfail, GLenum dppass);
sfail은 스텐실 테스트 실패시의 동작을 지정한다. dpfail은 스텐실 테스트는 성공했지만 깊이 테스트는 실패했을 때의 동작을 지정한다. dppass는 스텐실 테스트와 깊이 테스트를 모두 성공했을 때의 동작을 지정한다. 각각 다음과 같은 동작을 지정할 수 있다.
GL_KEEP: 현재값을 유지한다.GL_ZERO: 0으로 기록한다.GL_REPLACE: ref 비교값을 기록한다.GL_INCR: 값을 1증가시킨다.GL_INCR_WRAP: 값을 1증가시킨다. 최대값에 도달하면 0으로 돌아간다.GL_DECR: 값을 1감소시킨다.GL_DECR_WRAP: 값을 1감소시킨다. 0보다 작아지면 최대값으로 돌아간다.GL_INVERT: 비트 반전시킨다.
설명만 읽어서는 스텐실의 동작 방식을 이해하기 쉽지 않다. 다음 예제는 가위와 스텐실 기능을 테스트한다. 팝업 메뉴로 옵션을 바꿔 가며 결과를 비교해 보자.
#include <windows.h>
#include <gl/glut.h>
#include <stdio.h>
void DoDisplay();
void DoKeyboard(unsigned char key, int x, int y);
void DoMenu(int value);
GLfloat nx, ny;
BOOLEAN bScissor;
BOOLEAN bStencil;
BOOLEAN bEqual;
int APIENTRY WinMain(HINSTANCE hInstance,HINSTANCE hPrevInstance
,LPSTR lpszCmdParam,int nCmdShow)
{
glutInitDisplayMode(GLUT_RGB | GLUT_STENCIL);
glutCreateWindow("OpenGL");
glutDisplayFunc(DoDisplay);
glutKeyboardFunc(DoKeyboard);
glutCreateMenu(DoMenu);
glutAddMenuEntry("Scissor ON",1);
glutAddMenuEntry("Scissor OFF",2);
glutAddMenuEntry("Stencil ON",3);
glutAddMenuEntry("Stencil OFF",4);
glutAddMenuEntry("Equal",5);
glutAddMenuEntry("Not Equal",6);
glutAttachMenu(GLUT_RIGHT_BUTTON);
glutMainLoop();
return 0;
}
void DoKeyboard(unsigned char key, int x, int y)
{
switch(key) {
case 'a':nx -= 0.1;break;
case 'd':nx += 0.1;break;
case 'w':ny += 0.1;break;
case 's':ny -= 0.1;break;
}
glutPostRedisplay();
}
void DoMenu(int value)
{
switch(value) {
case 1:
bScissor=TRUE;
break;
case 2:
bScissor=FALSE;
break;
case 3:
bStencil=TRUE;
break;
case 4:
bStencil=FALSE;
break;
case 5:
bEqual=TRUE;
break;
case 6:
bEqual=FALSE;
break;
}
glutPostRedisplay();
}
void DoDisplay()
{
glClear(GL_COLOR_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
// 가위 테스트
if (bScissor) {
glEnable(GL_SCISSOR_TEST);
} else {
glDisable(GL_SCISSOR_TEST);
}
glScissor(10,10,150,150);
if (bStencil) {
glEnable(GL_STENCIL_TEST);
} else {
glDisable(GL_STENCIL_TEST);
}
// 스탠실 버퍼에 마킹만 한다.
glStencilFunc(GL_NEVER, 0x0, 0x0);
glStencilOp(GL_INCR, GL_INCR, GL_INCR);
// 수평 선 그음
glColor3f(1,1,1);
GLint arFac[] = { 1, 1, 1, 2, 3, 4, 2, 3, 2};
GLushort arPat[]={0xaaaa,0x33ff,0x57ff,0xaaaa,0xaaaa,0xaaaa,0x33ff,0x33ff,0x57ff };
glEnable(GL_LINE_STIPPLE);
glLineWidth(3);
GLfloat y;
GLint idx = 0;
for (y = 0.8; y > -0.8;y -= 0.2) {
glLineStipple(arFac[idx], arPat[idx]);
glBegin(GL_LINES); {
glVertex2f(-0.8, y);
glVertex2f(0.8, y);
}
glEnd();
idx++;
}
// 스텐실 값과 비교하여 특정 영역에만 출력한다.
glStencilFunc(bEqual ? GL_EQUAL:GL_NOTEQUAL, 0x1, 0xff);
// nx, ny 위치에 삼각형 그림
glColor3f(0,0,1);
glBegin(GL_TRIANGLES);
glVertex2f(nx + 0.0, ny + 0.5);
glVertex2f(nx -0.5, ny - 0.5);
glVertex2f(nx + 0.5, ny - 0.5);
glEnd();
glFlush();
}
별다른 제약 조건이 없다면 두 그림은 겹쳐서 출력된다. 가위 기능을 켜면 좌하단 (10, 10)좌표에서 150, 150만큼의 영역에만 출력되고 그 바깥은 잘린다.

가위가 지정하는 좌표는 윈도우 좌표이므로 창의 크기를 줄여도 제한되는 영역은 동일하다. 그래서 제한 영역보다 더 작게 윈도우를 만들면 모두 보이기도 한다.
스텐실 기능을 켜면 점선이 직접적으로 보이지 않는다. 점선을 그리기 전에 스텐실 테스트를 GL_NEVER로 지정했으므로 선은 결국 그려지지 않는 셈이다. 대신 스텐실 버퍼에 점선이 그려지는 영역이 1씩 증가하여 1의 값을 갖게 된다.
삼각형을 그릴 때는 스텐실 함수를 1과 같거나 다른 값으로 지정했으므로 삼각형의 모든 영역이 그려지지 않고 스템실 버퍼의 값과 비교하여 점선이 지나갔던 영역이나 또는 그 반대 영역만 그려진다. 직전에 그렸던 그림은 색상 버퍼에는 기록되지 않지만 스텐실 버퍼에 기록되어 다음 출력에 영향을 미친다.

복잡한 모양으로 스텐실을 만들어 둘 수 있어 임의의 모양으로 출력을 제한할 수 있다. 예를 들어 복잡한 무늬로 글자를 쓰고 싶다면 글자 모양을 스텐실 버퍼에 먼저 쓰고 이 버퍼에 글자가 지나간 부분에 대해서만 무늬를 칠하면 된다.





0개의 댓글