[번역] 음악에서 음정 (Interval) (2): 전위, 분류, 곁음정 등

전위

홑음정(simple interval; 옥타브보다 작거나 같은 음정)은 낮은 음정을 한 옥타브 올리거나 혹은 높은 음정을 한 옥타브 낮추어 전위(inversion)시킬 수 있습니다. 예를 들어, 낮은 C에서 높은 F까지의 4도는 F에서 더 높은 C까지의 5도로 전위될 수 있습니다.

 

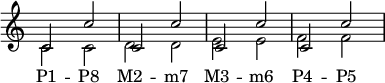
홑음정의 성질과 도수의 전위를 계산하는 두 가지 규칙이 있습니다.

1. 음정의 도수와 전위된 음정의 도수는 항상 합이 9가 됩니다(방금 주어진 예에서 4 + 5 = 9).
2. 장음정의 전위는 단음정이며 그 반대도 성립합니다. 완전음정의 전위는 완전입니다. 증음정의 전위는 감음정이며 그 반대도 마찬가지입니다. 겹증음정의 전위는 겹감음정이고 그 반대도 마찬가지입니다.
   • 장음정 ↔ 단음정
   • 단음정 ↔ 장음정
   • 완전음정 ↔ 완전음정
   • 증음정 ↔ 감음정
   • 감음정 ↔ 증음정
   • 겹증음정 ↔ 겹감음정
   • 겹감음정 ↔ 겹증음정

예를 들어 C에서 그 위의 E♭까지의 음정은 단 3도입니다. 방금 주어진 두 가지 규칙에 따라 전위된 E♭에서 위의 C까지의 간격은 장 6도입니다.

곁음정(복합 음정)은 옥타브보다 크기 때문에 곁음정의 전위는 항상 곁음정으로부터 결합된 홑음정의 전위와 동일합니다. (The inversion of any compound interval is always the same as the inversion of the simple interval from which it is compounded.)

비율(ratio)로 식별되는 음정의 경우 전위는 비율을 역으로 하고 비율이 1보다 커질 때까지 비율에 2를 곱하여 결정됩니다. 예를 들어 5:4 비율의 전위는 8:5 비율입니다.

반음의 수(semitone)로 식별되는 음정의 경우 전위는 12에서 해당 숫자를 빼서 얻습니다.

[심화] 음정 클래스(interval class)는 음정의 정수(Integer)와 그 전위 중 선택된 낮은 수이므로 음정 클래스는 전위될 수 없습니다.

 

 

음정의 분류 (Classification)

음정은 다양한 기준에 따라 묘사, 분류 또는 서로 비교할 수 있습니다.

 

선율(melody)과 화성(harmonic)

• 두 음이 동시에 들리는 경우 수직(vertical) 또는 화성(harmonic)
• 연속적으로 들리면 수평(horizontal), 선형(linear) 또는 선율(melody)입니다. 선율 간격은 상행(ascending)또는 하행(descending)일 수 있습니다.

 

온음계와 반음계 (Diatonic and chromatic)

일반적으로

• 온음 음정(diatonic interval)은 온음 음계의 두 음으로 구성된 음정입니다.
• 반음 음정(chromatic interval)은 반음계의 두 음으로 구성된 비온음계적(non-diatonic) 음정입니다.

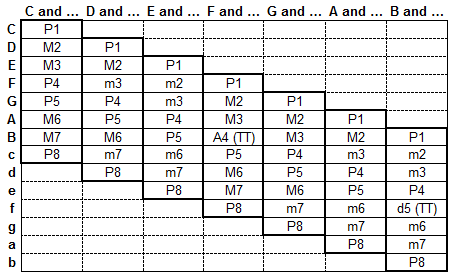
위의 표는 C 장조 음계(온음 음계)의 음으로 구성된 56개의 온음 음정을 나타냅니다. 이러한 음정은 다른 온음 음정과 마찬가지로 반음 음정의 음표로도 형성될 수 있습니다.

 

온음 음정과 반음 음정의 구분은 문헌에서 가변적인 온음계의 정의를 기반으로 하기 때문에 논쟁의 여지가 있습니다. 예를 들어, 음정 B–E♭(화성 c단조 음계에서 발생하는 감4도)는 화성적 단음계가 온음계로 간주되는 경우 마찬가지로 온음 음정으로 간주됩니다. 그 외의 경우는 반음 음정으로 간주됩니다. 자세한 내용은 본문(영어)을 참조하세요.

일반적으로 사용되는 온음계 정의(화성적 단조 및 선율적 단조 제외)에 따르면 모든 완전음, 장음 및 단음은 온음 음정입니다. 반대로 증음정, 감음정은 증 4도 및 감 5도를 제외하고 온음 음정이 아닙니다.

온음 음정과 반음 음정 사이의의 구분은 맥락에 따라 민감할 수도 있습니다. 위에서 언급한 C 메이저 스케일에 의해 형성된 56개의 음정은 때때로 C 메이저에 대한 온음 음정이라고 합니다. 다른 모든 음정은 C 장조에는 반음 음정이라고 불립니다. 예를 들어, A♭–E♭는 C장조음계에 A♭와 E♭가 포함되어 있지 않기 때문에 C장조의 반음 음정입니다. 그러나 A♭ 메이저 스케일과 같은 다른 것에는 온음 음정입니다.

 

협화음과 불협화음 (Consonant and dissonant)

협화음과 불협화음은 특정 음악적 효과의 안정감 또는 휴식(repose) 상태를 나타내는 상대적인 용어입니다. 불협화음정(dissonant interval)은 텐션을 일으키고 협화음정(consonant interval)으로 해결되고자 하는 욕구가 강한 음정입니다.

이 용어는 다른 구성 스타일의 사용과 관련이 있습니다.

• 15세기와 16세기 사용에서 완전 5도와 옥타브(완전 8도), 장 3도와 단 3도, 단 6도는 화음적으로 조화되는 것으로 간주되었고, 완전 4도를 포함하여 다른 모든 음정은 불협화음으로 간주되었습니다. 예를 들어, 아래의 3도의 경우(“6-3 화음”). 일반적 관행 기간(Common practice period; 고전 시대와 낭만 시대를 아우르는 1650년부터 1900년대까지의 기간을 뜻함)에는 협화 및 불협화음에 대해 말하는 것이 더 합리적이며 이전에 불협화음으로 간주되었던 특정 음정(예: 단 7도)이 특정 상황에서 허용되었습니다. 그러나 16세기 관습은 이 기간 동안 여전히 초보 음악가들에게 가르쳐졌습니다.
• 헤르만 폰 헬름홀츠(Hermann von Helmholtz, 1821-1894)는 불협화음이 비트(beat)의 존재로 인해 발생한다는 이론을 세웠습니다. von Helmholtz는 더 나아가 화성음의 상위 부분에 의해 생성된 박동이 기본음 사이의 박동을 생성하기에는 너무 멀리 떨어져 있는 음정에 대한 불협화음의 원인이라고 믿었습니다. von Helmholtz는 낮은 부분을 공유하는 두 개의 화성음이 더 적은 비트를 생성하기 때문에 더 협화음이 될 것이라고 간주했습니다. von Helmholtz는 중요한 효과를 낼 만큼 충분히 들리지 않는다고 믿었기 때문에 7도이상의 부분음은 무시했습니다. 이로부터 von Helmholtz는 옥타브, 완전 5도, 완전 4도, 장 6도, 장 3도, 단 3도를 협화음, 감음정 및 기타 음정을 불협화음으로 분류합니다.
• David Cope(1997)는 음정의 강도(interval strength), 협화음 또는 안정성이 배음렬(harmonic series)에서 근사적으로 위치가 낮을수록 더 강하거나, 위치가 높을수록 더 약하다는 이론을 제안했습니다.

위의 모든 분석은 수직(동시) 음정에 대한 것입니다.

 

홑음정 및 겹음정 (Simple and compound)

홑음정(단순 음정; simple interval)은 한 옥타브에 걸친 음정입니다(지난 글의 주요 음정 섹션 참조). 하나 이상의 옥타브에 걸친 음정을 겹음(복합 음정; compund interval)이라고 합니다. 홑음정에 하나 이상의 옥타브를 추가하여 얻을 수 있기 때문에 복합 음정이라고 합니다(자세한 내용은 아래 참조).

 

Steps and skips

(step, skip에 대응하는 한글 용어를 찾지 못했기 때문에 나중에 업데이트 하도록 하겠습니다.)

참고)

Step: 음이 2도로 이동
Skup: 음이 3도 이상으로 이동

선형(멜로디) 간격은 step 또는 skip로 설명될 수 있습니다. step 또는 conjunction motion은 스케일의 두 연속 노트 사이의 선형 음정입니다. 더 큰 음정은 skip(leap이라고도 함) 또는 disjunct motion이라고 합니다.  온음계에서 한 step는 단 2도(때때로 half step이라고도 함) 또는 장 2도(때때로 whole step라고도 함)이며, 단 3도 이상의 모든 음정은 모두 skip이라고 합니다.

예를 들어 C에서 D(장 2도)는 step이고 C에서 E(장 3도)는 skip입니다.

더 일반적으로, step은 음악적 라인에서 더 작거나 좁은 음정이며 skip은 더 넓거나 더 큰 음정입니다. 여기서 음정을 step와 skip로 분류하는 것은 튜닝 시스템과 사용된 pitch space에 의해 결정됩니다.

임의의 두 연속 피치 사이의 간격이 한 step 이하인 선율 동작(melodic motion), 덜 엄격하게 말하면, skip가 드문 경우를 단계적(stepwise) 또는 순차적(conjunct) 선율적 동작이라고 합니다. 반대의 경우를 skipwise 또는 도약적(disjunct) 동작이라고 합니다.

 

이명동음적 음정 (Enharmonic intervals)

 

두 음정이 서로 다른 방식으로 표기되는 동일한 피치를 포함하는 경우 협화적이거나 협화적으로 동등한 것으로 간주됩니다.

즉, 두 음정의 음표 자체가 협화적으로 동일한 경우입니다. 이명동음적 음정은 동일한 수의 반음 간격을 가지고 있습니다.

예를 들어, 아래 표에 나열된 네 개의 음정은 F♯와 G♭ 음이 동일한 피치를 나타내고 A♯와 B♭도 마찬가지이기 때문에 모두 화음적으로 동일합니다. 이 모든 음정은 4개의 반음에 걸쳐 있습니다.

피아노 건반에서 분리된 코드로 연주할 때 이러한 음정은 모두 동일한 두 건반으로 연주되기 때문에 귀로 구분할 수 없습니다. 그러나 음악적 맥락에서 이러한 음정이 포함하는 음의 온음적 기능(diatonic function)은 매우 다릅니다.

위의 논의는 일반적인 튜닝 시스템인 12음 평균율(12-TET)의 사용을 가정합니다. 그러나 다른 역사적 의미가 있는 튜닝 시스템에서는 F♯ 및 G♭와 같은 음 쌍의 피치가 반드시 일치하지 않을 수 있습니다. 이 두 음표는 12-TET에서 조화롭지만 다른 튜닝 시스템에서는 그렇지 않을 수 있다는 것입니다. 그러한 경우에 형성되는 음정도 조화롭지 않을 것입니다. 예를 들어 qurter-comma meantone에서 위의 예에 표시된 네 개의 음정이 모두 다를 수 있습니다.

 

미세 음정 (Minute intervals)

또한 반음계에서 찾을 수 없거나 고유한 이름을 가진 온음적 기능으로 레이블이 지정되지 않는 많은 미세 음정(minute intervals)이 있습니다. 그것들은 미분음(microtones)으로 설명될 수 있으며, 그것들 중 일부는 일부 조율 시스템에서 관찰되는 조율적으로 동등한 음 사이의 작은 불일치를 설명하기 때문에 comma로 분류될 수도 있습니다. 다음 목록에서 센트(cents) 단위의 간격 크기는 근사치입니다.

• 피타고라스 콤마 (Pythagorean comma)는 12개의 적절하게 조율된 완전 5도와 7옥타브 사이의 차이입니다. 이는 주파수 비율 531441:524288(23.5센트)로 표현됩니다.
  

  벤 조스턴의 표기법을 사용한 C에서의 피타고라스콤마. B♯+++보단 낮고 C♮보단 높은 음이다.

• Syntonic comma는 4개의 적절하게 조율된 완전 5도와 2개의 옥타브에 장3도를 더한 것의 차이입니다. 비율은 81:80(21.5센트)으로 표현됩니다.
• Septimal comma는 64:63(27.3 센트)이며 피타고라스식 또는 3 리미트 “7도”와 “화성적 7도”의 차이입니다.
• Diesis는 일반적으로 3개의 적절하게 조율된 장3도와 1옥타브 사이의 차이를 의미하는 데 사용됩니다. 비율은 128:125(41.1센트)로 표현됩니다. 그러나 다른 작은 음정을 의미하는 데에도 사용되었습니다.
• Diaschisma는 3옥타브와 4개의 적절하게 조율된 완전 5도와 2개의 적절하게 조율된 장3도 사이의 차이입니다. 비율은 2048:2025(19.6센트)로 표현됩니다.
• 스키즈마(스키즈마라고도 함)는 5옥타브와 8개의 적절하게 조율된 5도와 1개의 적절하게 조율된 장3도 사이의 차이입니다. 비율은 32805:32768(2.0센트)로 표시됩니다. 또한 피타고라스식과 통사적 쉼표의 차이점이기도 합니다. (분열된 메이저 3도는 단지 장 3도, 아래로 8/5, 위로 5 옥타브, C에서 F♭와 다른 분리입니다.)
• A kleisma is the difference between six minor thirds and one tritave or perfect twelfth (an octave plus a perfect fifth), with a frequency ratio of 15625:15552 (8.1 cents)
• Septimal kleisma은 5:4의 2개 장3도와 9:7의 septimal 장3도 또는 초장 3도(supermajor 3rd)가 옥타브를 초과하는 정도입니다. 비율 225:224(7.7센트).
• 4분음(a quarter tone)은 반음(semitone)의 반(half)입니다. 정확히 50센트입니다.

 

곁음정(복합 음정; Compund intervals)

곁음정(복합 음정)은 한 옥타브 이상에 걸쳐 있는 음정입니다. 반대로 최대 한 옥타브에 이르는 음정을 홑음정(simple interval)이라고 합니다.

일반적으로 곁음정은 모든 종류의 두 개 이상의 홑음정으로 이루어진 시퀀스 또는 “스택”으로 정의할 수 있습니다. 예를 들어, 곁음정의 장 3도라고도 하는 장 10도(한 옥타브 위에 두 개의 보표 위치)는 1옥타브에 장 3도 1개를 더한 것입니다.

모든 곁음정은 항상 하나 이상의 옥타브와 하나의 홑음정으로 분해될 수 있습니다. 예를 들어, 장 17도는 2옥타브와 장 3도 1개로 분해될 수 있으며, 5도 4개를 더해 만들어지더라도 곁음정의 장 3도라고 부르는 이유입니다.

온음계 DN₁, DN₂, …, DN_n이 있는 n개의 단순 음정으로 구성된 복합 음정의 온음계 DN_c는 다음과 같이 결정됩니다.

다음과 같이 쓸 수도 있습니다.

곁음정의 성질은 기반이 되는 홑음정의 성질에 따라 결정됩니다.

예를 들어, 복합 장 3도는 장 10도(1+(8-1)+(3-1) = 10) 또는 장 17도(1+(8−1)+(8−1)+(3−1) = 17)이고, 복합 완전 5도는 완전 12도(1+(8−1)+(5−1) = 12) 또는 완전 19도(1+(8−1)+(8−1)+(5−1) = 19)입니다.

두 옥타브는 16도가 아니라 15도입니다(1+(8-1)+(8-1) = 15). 마찬가지로 3옥타브는 22도입니다(1+3×(8-1) = 22).

 

주요 곁음정

여기에서 장 17도(28 반음)를 언급할 가치가 있습니다. 이 음정은 4개의 완전 5도 (7 × 4 = 28 반음)으로 구성되어 있어 완전 5도의 배수로 간주되거나 또는 2옥타브에 장 3도를 더한 것(12 + 12 + 4 = 28)입니다.

장 17도보다 큰 음정은 거의 나오지 않으며, 예를 들어 19도가 아닌 2옥타브 + 5도 와 같은 겹음정적 이름으로 언급됩니다.

 

화음의 음정

화음(chord)는 3개 이상의 음으로 구성된 세트입니다. 일반적으로 화음의 근음(root)이라고 하는 공통 음에서 시작하는 음정의 조합으로 정의됩니다. 예를 들어 메이저 3화음(triad)은 근음과 2개의 음정(장3도 및 완전 5도)으로 정의되는 3개의 음이 포함된 코드입니다. 때로는 단일 음정(dyad)도 화음으로 간주됩니다. 화음은 화음을 정의하는 음정의 성질과 수에 따라 분류됩니다.

 

화음의 특성과 음정의 특성

주요 화음의 특성은 메이저(장화음), 마이너(단화음), 오그멘티드(증화음), 디미니시드(감화음), 하프 디미니시드(half-diminished; 반감화음), 도미넌트(dominant; 딸림화음)입니다. 화음 특성에 사용되는 기호는 음정 특성에 사용되는 기호와 유사합니다. 또한 증화음에는 + 또는 aug, 감화음에는 ° 또는 dim, 반감화음에는 ø, 딸림화음에는 dom이 사용됩니다. (the symbol − alone is not used for diminished)

 

화음의 이름과 기호에서 구성 요소 및 음정 추론

화음의 이름이나 기호를 해독하는 주요 규칙은 다음과 같습니다.

1. 3화음(triad)의 경우 장단(Major or minor)은 항상 근음 위의 3도 음정을 나타내고 증감(Augmented or diminished) 은 항상 근음 위의 5도 음정을 나타냅니다. 해당 기호에 대해서도 마찬가지입니다 (예: Cm은 C^m3을 의미하고 C+는 C⁺⁵를 의미). 따라서, 3도 및 5도는 용어 및 대응하는 기호 3 및 5는 일반적으로 생략됩니다. 이 규칙은 모든 종류의 화음에 일반화될 수 있습니다. 위에서 언급한 특성이 근음 바로 뒤에 나타나거나 화음 이름 또는 기호의 시작 부분에 나타납니다. 예를 들어, 화음 기호 Cm 및 Cm⁷에서 m은 음정 m3을 나타내며 3은 생략됩니다. 이러한 특성이 근음 바로 뒤나 이름 또는 기호의 시작 부분에 나타나지 않으면 코드 특성이 아닌 음정 특성으로 간주해야 합니다. 예를 들어 CmM7(마이너 메이저 세븐스 코드)에서 m은 코드 특성이며 m3의 음정을 나타내고 M은 M7 음정을 나타냅니다. 화음의 특성 직후에 추가 음정의 도수가 지정되면 해당 간격의 품질이 코드 특성과 일치할 수 있습니다(예: CM⁷ = CM^M7). 그러나 항상 그런 것은 아닙니다(예: Cm⁶ = Cm^M6, C+⁷ = C+^m7, CM¹¹ = CM^P11). 자세한 내용은 해당 위키(영문)를 참조하십시오.
2. 상반되는 정보가 없으면 장 3도 음정과 완전 5도 음정(장3화음)이 암시됩니다. 예를 들어, C 코드는 C 메이저 3화음이고 Cm⁷이라는 이름은 규칙 1에 따른 단3도, 이 규칙에 따른 완전 5도, 아래의 정의에 따른 단7도를 의미합니다. 이 규칙에는 한 가지 예외가 있습니다(다음 규칙 참조).
3. 다섯 번째 음정이 diminished라면 세 번째 음정은 단음(minor)이어야 합니다. 이 규칙은 규칙 2보다 우선합니다. 예를 들어 Cdim⁷은 규칙 1에 의한 감 5도, 이 규칙에 의한 단 3도, 아래 정의에 의한 감 7도를 의미합니다.
4. 일반 음정 번호(예: “seventh chord”) 또는 코드 근음과 숫자(예: “C seven” 또는 C⁷)만 포함하는 이름 및 기호는 다음과 같이 해석됩니다.
   • 숫자가 2, 4, 6 등인 경우 해당 코드는 메이저 추가 톤(added tone) 화음(예: C⁶ = CM⁶ = Cadd⁶)이며 내재된 장3화음과 함께 여분의 장 2도, 완전 4도 또는 장 6도를 포함합니다.
   • 숫자가 7, 9, 11, 13 등인 경우 화음은 딸림음이며(예: C⁷ = C^dom7) 함축된 장3화음과 함께 다음 추가 음정 중 하나 이상을 포함합니다.
     • 단7도
     • 장9도
     • 완전 11도
     • 장 13도
   • 숫자가 5이면 화음(전통적인 의미의 화음이 아니라 dyad)는 파워 코드(power chord)입니다. 근음, 완전 5도 및 일반적으로 1 옥타브만 연주됩니다.

 

아래 표에는 일부 주요 화음(구성 요소 음정)에 포함된 음정과 이를 표시하는 데 사용되는 일부 기호가 나와 있습니다. 규칙 1을 적용하여 코드 이름 또는 기호에서 볼드체 글꼴의 음정 특성 또는 숫자를 추론할 수 있습니다. 기호 예에서 C는 화음의 근음으로 사용됩니다.

 

다른 튜닝 시스템에서 사용되는 음정의 크기

이 표에서는 네 가지 튜닝 시스템에서 사용되는 음정의 크기를 비교합니다. 비교를 용이하게 하기 위해 5-리미트 튜닝에서 제공하는 음정만 굵은 글꼴로 표시하고 센트 값은 정수로 반올림했습니다. 각각의 비동등(non-equal) 튜닝 시스템에서 정의에 따라 각 유형의 음정(반음 포함)의 크기는 간격을 시작하는 음에 따라 변경됩니다. 이것은 순정율의 특성입니다. 평균율에서는 음정이 서로 정확하게 조율되지 않습니다. 이것은 12음계에서 등간격을 사용하는 대가입니다. 단순화를 위해 일부 유형의 음정에 대해 테이블에는 하나의 값(가장 자주 관찰되는 값)만 표시됩니다.

1⁄4-comma meantone에서 11개의 완전 5도는 크기가 약 697센트(700 – ε센트, 여기서 ε ≈ 3.42센트)입니다. 12개의 5도의 평균 크기는 정확히 700센트(평균율에서와 같이)와 같아야 하므로 다른 하나의 크기는 약 738센트(700 + 11ε, 울프 5도(wolf fifth) 또는 감6도)여야 합니다. 8개의 장 3도는 약 386센트(400 – 4ε)이고 4의 크기는 약 427센트(400 + 8ε, 실제로 감 4도)이며 평균 크기는 400센트입니다. 요컨대 유니슨과 옥타브를 제외한 모든 음정 유형에서 유사한 크기의 차이가 관찰되며 모두 ε의 배수입니다(1/4 쉼표의 차이는 15도와 평균 5도를 의미함). 1⁄4-comma meantone은 장 3도만 생성하도록 설계되었지만 그 중 8개만 정확합니다(5:4, 약 386센트).

피타고라스 튜닝(Pythagorean tuning)은 더 작은 ε의 배수이기 때문에 더 작은 차이가 특징입니다(ε ≈ 1.96 센트, 피타고라스 5도와 평균 5도 사이의 차이). 여기에서 5도는 700센트보다 넓고 1⁄4-comma meantone를 포함하여 대부분의 meantone temperaments에서는 700보다 작은 크기로 조절됩니다.

5-리미트(5-limit) 튜닝 시스템은 완전 5도 스택이 아닌 구성 요소로 just tone과 반음만 사용하므로 음계 전체에서 훨씬 더 다양한 음정이 생성됩니다(각 종류의 음정에는 3~4개의 서로 다른 크기가 있음). 5 리미트 튜닝은 음정의 수를 최대화하도록 설계되었지만, 이 시스템에서도 일부 음정은 정확하지 않습니다. (예를 들어, 3의 5도, 5의 장 3도, 6의 단 3도는 정상음이 아닙니다. 또한 3의 장3도와 3의 단 3도는 울프 음정(영문)입니다).

위에서 언급한 5-리미트 튜닝 시스템에서 정의된 대칭 스케일 1은 단지 인토네이션을 얻기 위한 유일한 방법이 아닙니다. 더 나은 음정 또는 평균율에 더 가까운 음정을 구성하는 것이 가능하지만 위에 나열된 대부분의 음정은 역사적으로 동등한 맥락에서 사용되었습니다. 특히 비대칭 버전의 5리미트 튜닝 스케일은 마이너 7도에 대해 더 순수한(juster) 값을 제공합니다(16:9가 아닌 9:5). 더욱이 3온음(tritone; 증4도 또는 감5도)은 다른 더 순수한 비율을 가질 수 있습니다. 예를 들어, 7:5(약 583센트) 또는 17:12(약 603센트)는 증4 도에 대한 가능한 대안입니다. 화음 7도(harmonic 7th)라고도 알려진 7:4 음정(약 969센트)은 음악 이론의 역사를 통틀어 논쟁거리였습니다. 평균율의 단7도보다 31센트 더 평평(flatter)합니다.

 

음정의 근 (Interval root)

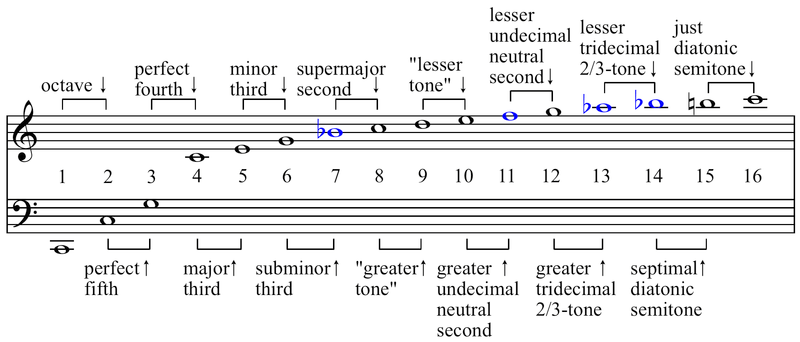
음정은 일반적으로 낮은 위치의 음표와 관련하여 지정되지만 David Cope와 Hindemith는 둘 다 음정의 근(interval root)의 개념을 제안했습니다. 음정의 근을 결정하려면 배음렬(harmonic series)에서 가장 가까운 근사값을 찾습니다. 완전 4도의 근은 가설의 배음렬(hypothetical harmonic series)에서 근의 옥타브이기 때문에 가장 높은 음표(top note)입니다. 온음계로 번호가 매겨진 모든 홀수 음정의 하단 음은 모든 짝수 음정의 상단과 마찬가지로 근입니다. 따라서 음정 모음 또는 화음의 근은 가장 강한(strongest) 음정의 음정 근에 의해 결정됩니다.

그 유용성에 관해서, Cope는 전통적으로 “submediant six-five chord”(대중 용어로 장6화음) 또는 첫 번째 전위의 7화음(아마도 mediant V/iii의 dominant). 화음의 가장 강한 음정(CEGA에서 첫 번째 전위)의 음정 근에 따르면 완전 5도(C–G)는 토닉인 하단의 C입니다.

 

음정 사이클 (Interval Cycle)

음정 사이클, “초기 피치 클래스로 돌아가는 시리즈에서 단일 반복 간격 전개”, 간격을 구별하기 위해 간격 클래스 정수와 함께 사이클에 문자 “C”를 사용하여 George Perle에 의해 표기됩니다. 따라서 감7화음은 C3이고 증3화음은 C4가 됩니다. 조옮김을 구별하기 위해 위 첨자를 추가할 수 있으며, 0-11을 사용하여 주기에서 가장 낮은 피치 등급을 나타냅니다.

 

(계속됩니다.)