코딩테스트: 쉬운 계단수 (백준 10844)

문제: 쉬운 계단수

• https://www.acmicpc.net/problem/10844

45656이란 수를 보자. 이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다. N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

• 입력: 첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
• 출력: 첫째 줄에 정답을 1,000,000,000(10억)으로 나눈 나머지를 출력한다.

예제 입출력

• 1 => 9
• 2 => 17

해답

Python 3

n = int(input())
divisor = 1000000000
dp = [[0] * 10 for _ in range(101)]

for i in range(1, 10):
    dp[1][i] = 1

for i in range(2, n + 1):
    for j in range(10):
        if j == 0:
            dp[i][j] = dp[i - 1][1] % divisor
        elif j == 9:
            dp[i][j] = dp[i - 1][8] % divisor
        else:
            dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % divisor

print(sum(dp[n]) % divisor)

Swift

let n = Int(readLine()!)!, divisor = 1000000000
var dp = Array(repeating: Array(repeating: 0, count: 10), count: 101)
for i in 1...9 {
    dp[1][i] = 1
}

for i in stride(from: 2, through: n, by: 1) {
    for j in stride(from: 0, through: 9, by: 1) {
        switch j {
        case 0:
            dp[i][j] = dp[i-1][1] % divisor
        case 9:
            dp[i][j] = dp[i-1][8] % divisor
        default:
            dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % divisor
        }
    }
}

print(dp[n].reduce(0, +) % divisor)

• 동적 프로그래밍 (Dynamic Programming)을 사용합니다.
• DP[자리수][맨_끝자리에_오는_수] 의 2차원 배열을 사용하며, 맨 끝자리에 오는 수에 따라 점화식을 다르게 지정합니다.
  • 0인 경우 dp[i][j] = dp[i-1][1]
  • 9인 경우 dp[i][j] = dp[i-1][8]
  • 그 외의 경우 dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1])
  • 점화식 도출 과정은 풀이 섹션에 있습니다.
• 중간 계산 과정에서 산술 오버플로(arithmetic overflow)를 방지하기 위해 나머지를 취하며 (x % divisor), 마지막 계산 과정에서 요구하는 답을 얻기 위해 한 번 더 나머지를 취합니다.
  • 이에 대한 자세한 설명은 참고 섹션에 있습니다.

풀이

먼저 계단수가 얼마나 만들어질 수 있는지 경우의 수를 따집니다.

• 자릿수별로 살펴볼 때, 자리수 = 1인 경우 0을 제외한 나머지 숫자는 계단수입니다.
  • 문제에서 한자리에 대한 구체적인 언급은 없습니다. 한자리인 경우 인접한 다른 자릿수가 없습니다.
  • 그러나 예제 입출력에서 1 => 9가 있었기 때문에 이를 토대로 한 자리 숫자는 1부터 9까지 계단수라고 정의합니다.
  • 경우의 수는 9입니다.
• 모든 계단수에서 0은 맨 앞에 위치할 수 없고, 1~9는 맨 앞에 위치할 수 있습니다.
• 자리수 = 2 인 경우
  • 마지막 자리가 9일때, 앞에는 8만 올 수 있으므로 경우의 수는 1입니다. (89)
  • 마지막 자리가 0일때, 앞에는 1만 올 수 있으므로 경우의 수는 1입니다. (10)
  • 마지막 자리가 1일때, 앞에는 2만 올 수 있으므로 경우의 수는 1입니다. (21)
  • 마지막 자리가 (2~8)일때, 앞에는 (1~7)과 (3~9)가 올 수 있으므로 경우의 수는 2입니다.
    • 예를 들어 마지막 자리가 4인 경우 (34, 54)입니다.
• 자리수 = 3인 경우
  • 마지막 자리가 9일때, 앞에는 8만 올 수 있고
    • 8 앞에는 7과 9가 올 수 있으므로
    • 가능한 경우는 (789, 989), 경우의 수는 2입니다.
  • 마지막 자리가 0일때, 앞에는 1만 올 수 있고
    • 1 앞에는 2만 올 수 있으므로
    • 가능한 경우는 (210), 경우의 수는 1입니다.
  • 마지막 자리가 1일때, 앞에는 2만 올 수 있고 (=> 맨 앞에는 0이 올 수 없습니다.)
    • 0 앞에는 1만 올 수 있고
    • 2 앞에는 1, 3이 올 수 있으므로
    • 가능한 경우는 (102, 121, 321), 경우의 수는 3입니다.
  • 마지막 자리가 2일때, 앞에는 1과 3이 올 수 있고
    • 1 앞에는 2만 올 수 있고
    • 3 앞에는 2, 4가 올 수 있으므로
    • 가능한 경우는 (212, 232, 432), 경우의 수는 3입니다.
  • 마지막 자리가 (3~8)일때, 앞에는 앞에는 (2~7)과 (4~9)가 올 수 있고,
    • 이 경우 각각 앞에는 두 개의 숫자가 올 수 있으므로
      • 예를 들어 4 앞에는 3과 5가 올 수 있습니다.
    •  경우의 수는 4가 됩니다.
      • 예를 들어 마지막 자리가 4인 경우 (234, 434, 454, 654) 가 가능한 경우입니다.

같은 자리수라도 마지막 자리에 따라 나올 수 있는 경우의 수가 달라지므로 1차원적으로 다룰 수는 없습니다. 테이블 표(2차원 배열)를 그려서 생각해봅니다.

• 세로축은 자리수이며, 가로축은 맨 끝에 오는 숫자를 뜻합니다.
  • 테이블의 각 칸은 경우의 수입니다.
  • 세로축은 i, 가로축은 J로 놓고 2차원 배열을 사용합니다.
  • 예를 들어 DP[2][0]의 값은 하늘색 칸의 1이며, DP[2][1]은 분홍색 칸의 1입니다.
• 자리수 0은 0으로 초기화합니다. (표의 - 부분)
  • 자리수가 0인 경우는 있을 수 없으므로 경우의 수는 0입니다.
  • 자리수가 0인 경우는 일반화된 점화식에서 필요합니다.
• 자리수 1은 앞에서 언급했듯이 경우의 수는 1입니다.
  • 자리수가 1인데 맨 뒷자리가 0인 경우는 성립할 수 없으므로 0으로 둡니다.
  • 점화식을 따라 DP[1-1][1] = 0을 가져오는 것으로 생각할 수도 있습니다.
• 자리수 2와 3도 똑같이 채웁니다.
• 여기서 규칙을 발견할 수 있습니다. 규칙에 따라 도출된 점화식을 이용해 계산합니다.
  • 맨 끝 숫자가 0인 경우에는 앞에 1밖에 올 수 없으므로 이전 자리수의 경우의 수 중 맨 끝이 1인 자릿수를 가져옵니다.
    • DP[i][0] = DP[i - 1][1]
    • i=1, j=0인 경우에는 DP[0][1] = 0에서 가져옵니다.
  • 맨 끝 숫자가 9인 경우에는 앞에 8밖에 올 수 없으므로 이전 자리수의 경우의 수 중 맨 끝이 8인 자릿수를 가져옵니다.
    • DP[i][0] = DP[i - 1][8]
  • 나머지 경우는 앞에 두 숫자가 올 수 있으므로 이전 자릿수에서 j-1, j+1인 경우의 수를 가져와서 더해줍니다. (대각선 화살표 참조)
    • DP[i][j] = DP[i - 1][j - 1] + DP[i - 1][j + 1]
    • 표의 경우 초록색, 노란색 칠한 곳이 해당 부분입니다.
    • 색칠하지 않은 영역도 마찬가지로 똑같은 규칙이 적용됩니다.
    • 앞에서 경우의 수를 도출하는 과정에서는 앞의 숫자가 2인 경우와 3~8인 경우를 다르게 취급했지만, 일반화된 점화식에서는 맨 끝 숫자가 2인 경우 앞 숫자가 1인 경우의 수와 3인 경우의 수를 더하고, 맨 끝 숫자가 3인 경우 앞 숫자가 (2, 4)인 경우의 수를 더하므로 동일한 식으로 계산할 수 있습니다.

참고: 나머지를 중간 계산과정에서도 해야하는 이유

결론부터 말하자면, 중간에 나머지를 안하면 산술 오버플로(arithmetic overflow)라는 유형의 런타임 에러가 발생하기 때문입니다.

나머지를 하지 않은 상태에서 문제에서 요구하는 최대값인 n = 100을 입력하면 다음과 같이 계산됩니다.

예) 중간 계산 과정에서 나머지를 하지 않은 경우 (=> 컴파일러 터짐)

• dp[68][2] = 8,833,413,110,019,436,605
• dp[67][1] = 3,292,956,562,874,470,358, dp[67][3] = 5,540,456,547,144,966,247
• dp[68][3] = 산술 오버플로우 (Swift runtime failure: arithmetic overflow)
•   => 9,770,621,288,303,265,298으로 Int(64비트)의 최대 범위인 9,223,372,036,854,775,807을 넘어선다.
• dp[67][2] = 4,230,164,741,158,299,051, dp[67][4] = 5,540,456,547,144,966,247

읽을수도 없는 천문학적인 숫자가 나오면서 for문의 i = 68번째에서 산술 오버플로가 발생합니다. 중간 계산과정에서 나머지를 하면 산술 오버플로를 방지할 수 있습니다.

예) 중간 계산 과정에서 나머지를 한 경우

• dp[68][2] = 19,436,605
• dp[67][1] = 874,470,358, dp[67][3] = 144,966,247
• dp[68][3] = 303,265,298 (=> 산술 오버플로 발생 안함)
• dp[67][2] = 158,299,051, dp[67][4] = 144,966,247

동일한 배열 주소에서 값 차이가 확연하게 벌어진 것을 알 수 있습니다.

그러면 중간에 했는데 마지막에 나머지는 왜 또 하나요?

나머지 공식이 성립해야 하기 때문입니다. 나머지 연산자 성질 중에 다음과 같은 공식이 있습니다.

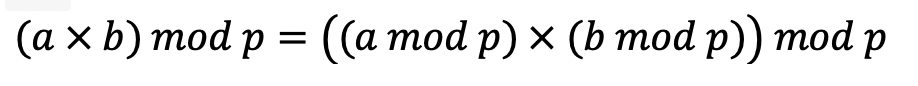
따라서 위 코드의 계산 결과는 최종 결과에도 나머지를 해야만 성립하게 됩니다.

예를 들어 n = 50인 경우 중간 나머지를 하지 않았을 때와, 중간 나머지를 했을 때 최종적인 답의 계산 과정은 다음과 같습니다.

중간 나머지를 했더라도 나머지 공식에 의해 최종합은 문제에서 원하는 답이 아니므로, 마지막 최종 결과에서도 나머지를 다시 해서 원하는 결과를 만들어야 합니다.