Swift(스위프트): 비트 연산자 (Bit Operator)

이 글은 자바스크립트(JavaScript): 비트 연산자 (Bit Operator) 포스트에서 자바스크립트를 Swift로 변경하고 내용을 보강하였습니다.

 

소개

비트 연산자란 2진수(binary)를 연산할 때 사용하는 연산자입니다.

예를 들어 십진법으로 표기한 정수 70을 이진법 표기로 변환하면

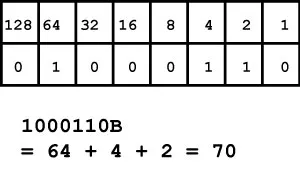
0100 0110B 가 되는데, 이 이진법으로 변환된 값을 기준으로 연산을 수행하는 연산자가 비트 연산자입니다.

이하 별도의 표기법이 없는 경우는 전부 십진법 숫자이며, 이진법은 숫자 뒤에 B가 붙어 있습니다.

 

Swift에서 이진법으로 입력하기

먼저 Swift에서 이진법으로 입력하는 방법을 알아보겠습니다.

• 숫자 앞에 0b 접두사를 붙입니다.
• 숫자 중간에 _를 붙여 자리를 구분할 수 있습니다. (보통 4자리씩 끊으며, 편의를 위해 사용되는 구분자이므로 아무 곳에 넣어도 상관없습니다.)

 

8비트 정수(Int8) 2를 이진법으로 입력하는 방법은 아래와 같습니다. 자료 타입은 별도이 지정이 없다면 Int로 취급됩니다.

// 2에 대한 이진법 표기 (1) -> Int
0b0000_0010

// 2에 대한 이진법 표기 (2) -> Int
0b0_000_1_0_

이와 같은 표기 방법을 Numeric Literals 표기법이라고 합니다.

 

음의 정수 (Negative Ineger)를 이진법으로 입력

이진법 표기에서 2의 보수를 이용해 음수 표기를 할 수 있습니다만, 이러한 조정된 이진수를 그대로 입력하면 컴파일러가 양수로 판단하기 때문에 오버플로 에러가 발생합니다.

음수를 입력하려면 Int(bitPattern:) 파라미터를 이용합니다. Int8, Int16, Int32, Int64 등으로 대체할 수 있습니다.

참고) 자료형 Int는 CPU에 따라 32비트 프로세서에서는 32비트, 64비트 프로세서에서는 64비트로 표현됩니다. 현재 Swift를 이용하는 OS들은 대부분 64비트 CPU에서 동작하므로 Int는 64비트로 취급됩니다.

// Signed Integer: -2 (1111 1110B) 입력
// 직접 0b1111_1110를 입력하려고 하면 254로 인식해서 overflow됨
// https://stackoverflow.com/questions/58617839

let minus2 = Int8(bitPattern: 0b1111_1110)

 

비트 연산자 (Bit Operator)

자주 사용되는 비트 연산자로 AND, OR, XOR, NOT, SHIFT 등이 있습니다.

 

1: AND( & ) 연산

AND 연산은 두 개의 숫자(값이)를 각 비트마다 AND 연산합니다. AND 연산은 곱연산으로 두 비트가 모두 1일 경우에만 1를 반환하며, 두 비트 중 하나라도 0이라면 0를 반환합니다.

• 1 & 1 = 1
• 1 & 0 = 0
• 0 & 1 = 0
• 0 & 0 = 0

 

70(100 0110B)과 54(11 0110B)의 AND 연산을 수행해 보겠습니다.

70 & 54
// 결과: 6

왜 6(110B)이 나올까요? 70과 60을 이진법으로 변환시킨 뒤 계산해보면 이해할 수 있습니다.

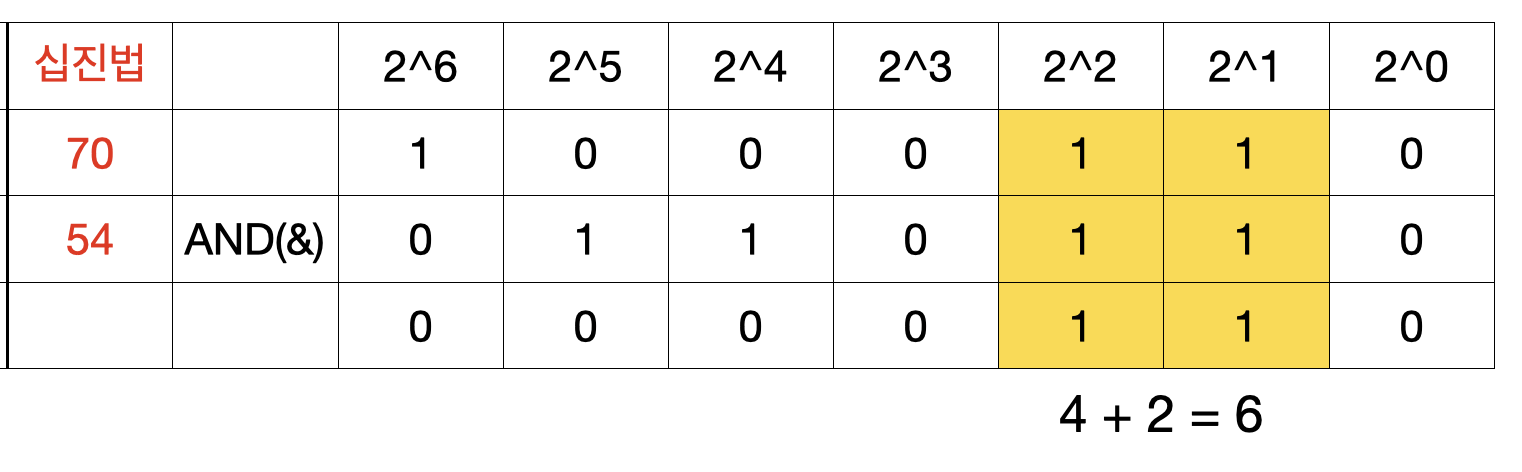
위 표처럼 십진법을 이진법으로 변환시킨 뒤, 각 자릿수마다 AND 연산을 한 뒤 나온 비트들을 다시 십진법 표기로 변환하면 6이 나오는 것을 알 수 있습니다.

 

예제: 특정 자리의 비트수가 1인지 확인

AND 연산은 양쪽 모두가 1인 경우 외에는 전부 0을 반환합니다. 이 속성을 이용해 숫자의 어떤 자리수가 1인지 여부를 확인할 수 있습니다.

204(1100 1100B)의 각 자릿수가 1인지 확인하기

for i in 0..<8 {
    let digit = (8 - 1) - i
    let powed = NSDecimalNumber(decimal: pow(2, digit))
    let isNumberOne = (Int(truncating: powed) & 204) != 0
    print(digit, isNumberOne)
}

• NSDecimalNumber와 Int(truncating:)을 사용한 이유는 pow(x, y) 함수는 Decimal 타입을 반환하는데, 해당 타입은 Int형과 계산 작업을 수행할 수 없기 때문입니다.
  • Decimal 타입을 NSDecimalNumber으로 변환합니다.
  • NSDecimalNumber으로 반환된 powed의 값을 Int(truncating:)을 사용하여 Int로 변환합니다.

 

204와 2^7 = 128(1000 0000B)를 AND 연산하면 맨 앞의 1을 제외하고는 공통되는 비트가 없으므로 나머지는 전부 0이 됩니다. 따라서 204 & 128의 연산 결과는 128(1000 0000B)이 됩니다.

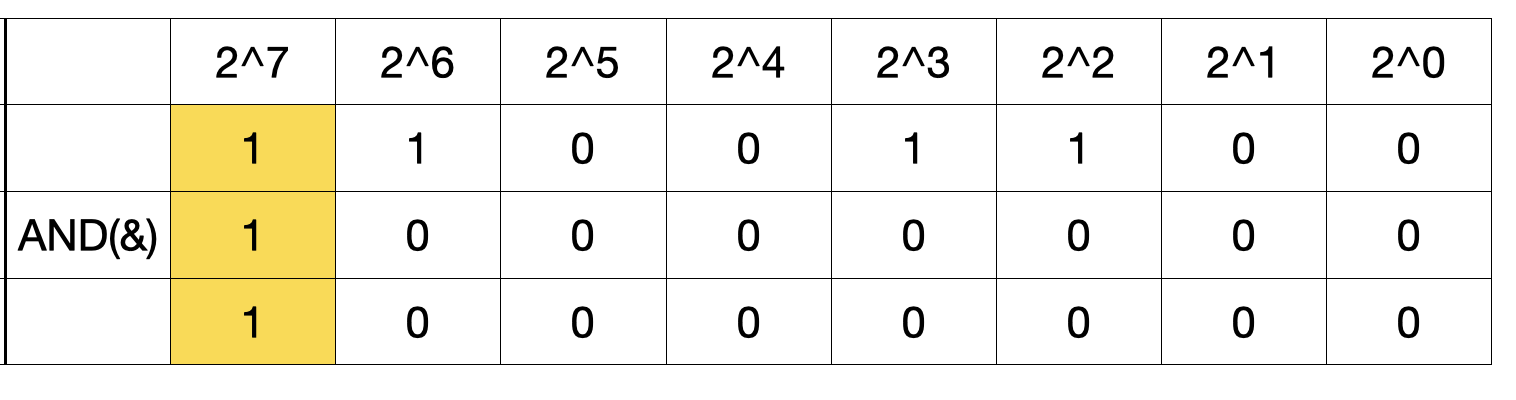
204와 2^5 = 32(0010 0000B)를 AND 연산하면 공통되는 부분이 하나도 없으므로 연산 결과는 0이 됩니다.

위의 패턴으로 볼 때 각 자리값마다 연산 결과가 0이 아닌 경우 해당 자릿수는 1이므로 true, 아니라면 false를 반환합니다.

비트 필드 또는 비트 플래그라 불리는 데이터 저장 기법이 있는데, 비트 필드를 사용할 때 체크 여부를 이러한 AND 연산으로 판별합니다.

후술할 SHIFT 연산자를 이용하는 방법은 다음과 같습니다.

var bitFlag = 1
var checkNumber = 0b0100_1010
for _ in 1...8 {
    print(bitFlag, (bitFlag & checkNumber) != 0)
    bitFlag = bitFlag << 1
}

• for 문이 반복되면서 bitFlag가 왼쪽 시프트 연산을 수행해 1, 2, 4, 8, 16, 32, 64, 128로 증가하며, 이를 확인할 숫자와 곱한 뒤 그 결과가 0이 아니라면 true, 0이라면 false로 판별합니다.

 

2: OR( | ) 연산

OR 연산은 두 개의 숫자를 각 비트마다 OR 연산합니다. OR 연산은 합연산으로 두 비트 중  하나라도 1일 경우에는 1를 반환하며, 두 비트가 모두 0인 경우에만 0를 반환합니다.

• 1 | 1 = 1
• 1 | 0 = 1
• 0 | 1 = 1
• 0 | 0 = 0

 

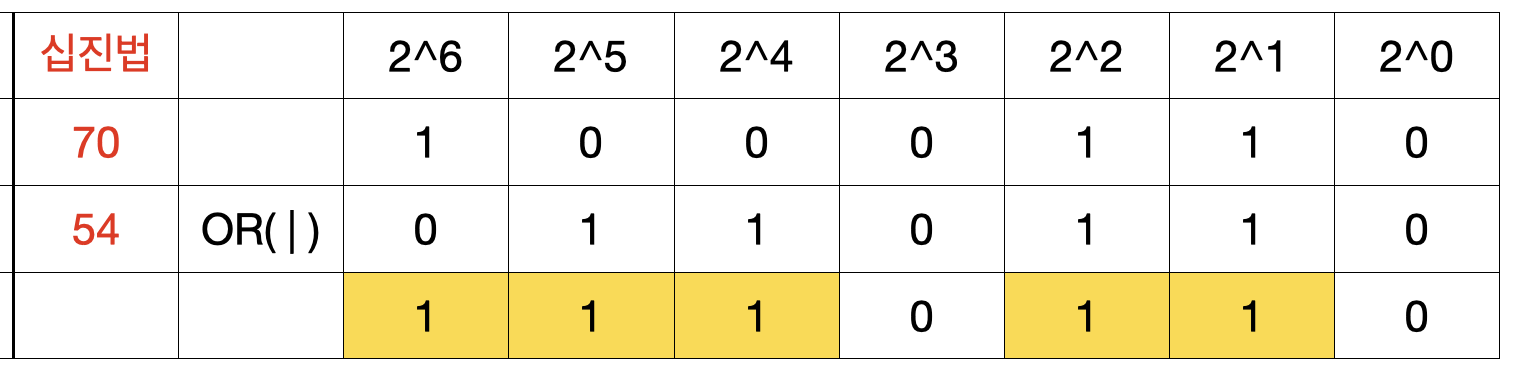
70(100 0110B)과 54(11 0110B)의 OR 연산 방법은 다음과 같습니다.

70 | 54
// 결과: 118

AND 연산과 다르게 118(111 0110B)이 나오는 이유는 아래 그림을 보면 알 수 있습니다.

3: XOR( ^ ) 연산 – Exclusive OR

두 비트의 값이 같은 경우 0를 반환하며, 두 비트값이 다른 경우에는 1를 반환합니다.

참고로 두 값을 더한 뒤 mod(%) 2를 했을때의 값과 동일합니다.

• 1 ^ 1 = 0
• 1 ^ 0 = 1
• 0 ^ 1 = 1
• 0 ^ 0 = 0

 

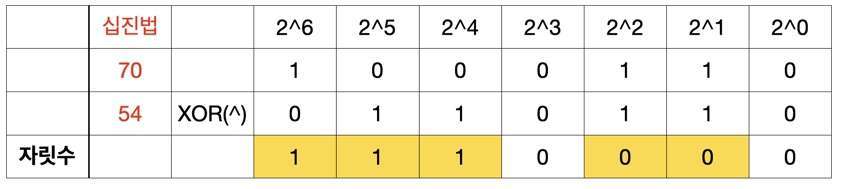
70(1000 110B)과 54(11 0110B)의 XOR 연산 방법은 다음과 같습니다.

70 ^ 54
// 결과: 112

112 (111 0000B)가 나온 이유는 다음과 같습니다.

 

4: NOT( ~ ) 연산

NOT 연산은 1을 0으로, 0을 1로 반전시킵니다.

자바스크립트 내에서 음수의 비트 표기법에 의해 NOT 연산자를 수행하면 해당 양수/음수 부호와 반대되는 값이 나옵니다. (모든 비트를 반전 = 1의 보수로 변환)

/*
 - 70(0100 0110B)에 ~를 붙이면 비트를 반전시킨다.
 - 반전된 비트 1011 1001은 2의 보수 방식의 음수이다.
 - 십진수로 변환하면 1011 1000 -> 0100 0111 -> -71
 */
~70
// 결과 : -71

~70의 결과는 71이 나오는데, 그 이유는 반전된 비트 값을 2의 보수 방식의 이진법 음수로 취급하기 떄문입니다.

참고

• 2진수의 음수표현 (부호 절대값, 1의 보수, 2의 보수)
• 자바(Java) 예제: 1 또는 2의 보수 구하기

 

2의 보수를 이해하려면 1의 보수에 대한 이해가 먼저 필요합니다. 8비트를 기준으로 살펴보겠습니다.

먼저 1의 보수란 비트를 ~ 연산시켜서 나온 반전된 비트값입니다. (정확히 말하면 1111 1111B - x의 결과값이나 비트 반전으로 이해하는 것이 편합니다.)

• 70(0100 0110B)의 1의 보수는 비트 반전 결과값인 1011 1001B 입니다.

 

2의 보수는 1의 보수에 1을 더한 결과값입니다. (1000 0000B - x의 결과값입니다.)

• 1011 1001B + 1 = 1011 1010B

 

이를 바탕으로 2의 보수로 표현된 비트값 x에서 어떤 음수를 표현하는지 역으로 알아낼 수 있습니다.

1. x에서 1을 뺍니다 (-1을 더합니다).
2. 1의 결과값을 비트 반전합니다.
3. 해당 비트에서 나온 양수값에 -(마이너스)를 붙이면 됩니다.

 

예) 1110 0111B (2의 보수 방식의 음수)를 십진법으로 변환

1. 1을 뺀다 → 1110 0110
2. 비트 반전 → 0001 1001
3. 0001 1001 → 십진법으로 변환하면 +25 → (-) 붙이면 -25 가 결과이다.

 

이를 토대로 70(0100 0110B)에 ~를 붙이면 1011 1001B(2의 보수로 표시된 음수)가 되고,  이것을 십진법으로 변환하면 -71이 나오는 것입니다.

– 70(0100 0110B)에 ~를 붙이면 비트를 반전시킨다.

– 반전된 비트 1011 1001은 2의 보수 방식의 음수이다.

– 십진수로 변환하면 1011 1000 → 0100 0111 → -71

 

5: 왼쪽(<<) / 오른쪽(>>) SHIFT 연산

왼쪽 SHIFT (<<) 연산자는 모든 비트를 왼쪽으로 x 칸씩 이동시킵니다. 이동 범위를 초과하는 값은 버려지고, 새로 생긴 빈 칸은 0으로 채워집니다.

아래 코드는 70(100 0110B)의 모든 비트를 왼쪽으로 2칸씩 이동하라는 의미로, 결과는 280(1 0001 1000B)이 나옵니다. 왼쪽으로 2칸씩 이동하면서 새로 생긴 끝의 2자리는 0으로 채워집니다.

70 << 2
// 결과: 280

 

오른쪽 SHIFT (>>) 연산자는 모든 비트를 오른쪽으로 x 칸씩 이동시킵니다. 이동 범위를 초과하는 부분은 버려집니다.

아래 코드는 70(100 0110B)의 모든 비트를 오른쪽으로 2칸씩 이동하라는 의미로, 결과는 17(1 0001B)이 나옵니다. 오른쪽으로 2칸씩 이동하면서 맨 끝자리 2개의 비트(2^1 자리, 2^0 자리)는 버려집니다.

70 >> 2
// 결과: 17