자바(Java) 예제: 재귀 호출(Recursive Call, 재귀 함수, 재귀 알고리즘)

재귀호출 설명

재귀(Recursion) 알고리즘이란 어떠한 문제를 자기 자신을 호출하여 해결하는 과정을 말합니다.

링크

예제 1: 코드 실행 추적

다음은 정보처리산업기사에서 출제된 문제입니다. 다음 코드의 실행 결과는?

public class RecursiveExample {
    
    public static int recursive(int n) {
        int i;
        if (n < 1)    return 2;
        else {
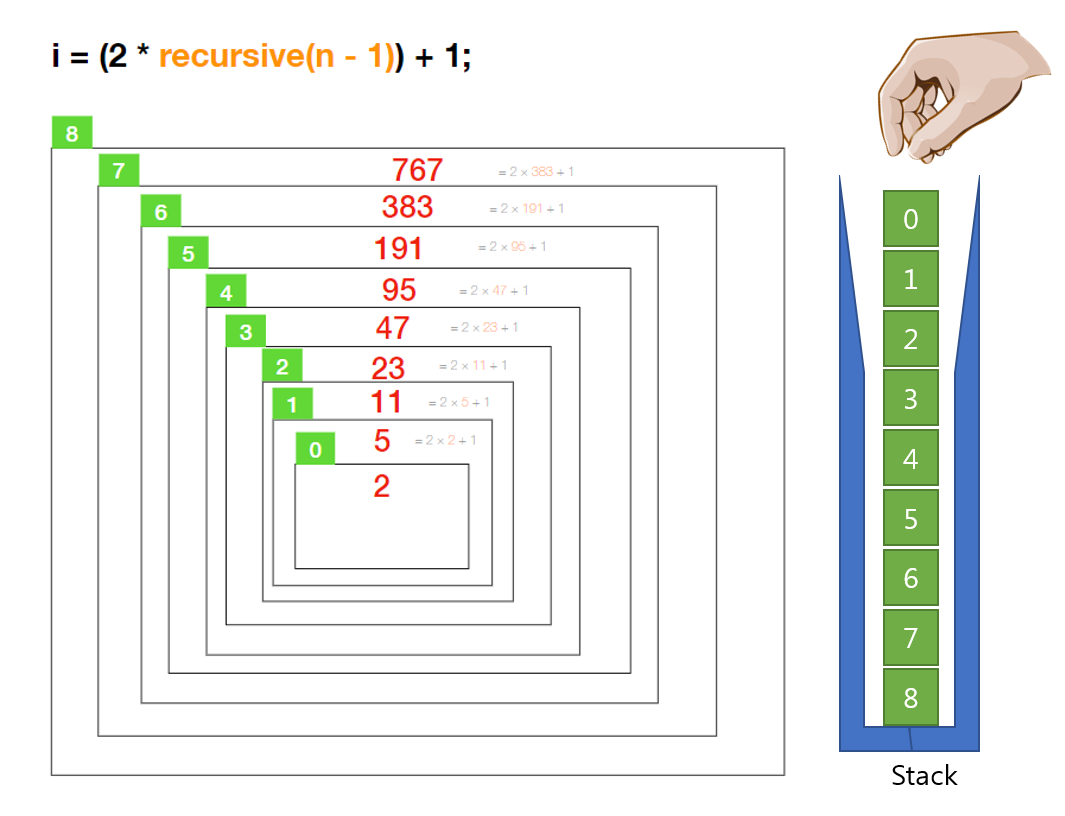
            i = (2 * recursive(n - 1)) + 1;
            System.out.printf("%d\n", i);
            return i;
        }
    }
    
    public static void main(String[] args) {
        recursive(8);
    }
 
}

답:

recursive(n-1) 부분이 계속 호출되면서 값을 반환합니다. 최후의 입력값(0)부터 recursive 함수(메소드) 자체에 반환된 값을 대입해 결과를 연쇄적으로 나열하면 됩니다.

n이 0인 경우 2를 리턴하고 밑으로는 더 이상 진행되지 않습니다.

예제 2: 팩토리얼

package blog.recursive;

public class FactorialExample {
  
  private static int factorial(int n) {
    if(n <= 1) {
      return 1;
    }
    
    return n * factorial(n - 1);
  }
  
  public static void main(String[] args) {
    for(int i = 1; i <= 10; i++) {
      System.out.printf("%d! = %d\n", i, factorial(i));
    }
  }

}

예제 3: 배열의 합 계산 (Arrays.copyOfRange 이용)

package blog.recursive;

import java.util.Arrays;

public class SumOfArray {
  private static int doSum(int[] array) {
    if(array.length <= 1) {
      return array[0]; 
    }
    // Arrays.copyOfRange(array, 시작 인덱스, 끝 인덱스);
    // 시작 인덱스는 포함, 끝 인덱스는 포함하지 않음
    int[] nextTarget = Arrays.copyOfRange(array, 1, array.length);
    return array[0] + doSum(nextTarget) ;
  }

  
  public static void main(String[] args) {
    int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; 
    System.out.println(doSum(array));
    
    int[] array2 = new int[10];
    for(int i = 0; i < array2.length; i++) {
      int rndNum = (int) (Math.random() * 100 + 1);
      array2[i] = rndNum;
    }
    // for문 없이 배열 출력
    System.out.println(Arrays.toString(array2));
    System.out.println(doSum(array2));
    
  }
}

예제 4: 회문 판별 (스트링 자르기 이용)

회문(palindrome; 回文: madam이나 nurses run처럼 앞에서부터 읽으나 뒤에서부터 읽으나 동일한 단어나 구)을 판별할 수 있는 프로그램입니다.

package blog.recursive;

public class Palindrome {
  
  private static boolean checkPalindrome(String word) {
    
    if(word.length() <= 1) {
      return true;
    }
    
    if(word.charAt(0) == word.charAt(word.length() - 1)) {
      // substring(beginIndex, endIndex) -> endIndex는 포함하지 않음
      return checkPalindrome(word.substring(1, word.length() - 1));
    } else {
      return false;
    }
  }
  
  public static void main(String[] args) {
    System.out.println(checkPalindrome("level"));
    System.out.println(checkPalindrome("poop"));
    System.out.println(checkPalindrome("leval"));
  }
}

예제 5: 패턴으로 결과 찾기

f(n) = f(n-1) + f(n-2) + f(n-3) 이고, f(1) = 1, f(2) = 2, f(3) = 4 인 것이 알려진 경우 f(n)을 구하는 프로그램 작성

package blog.recursive;

public class Pattern {
  private static int doCalc(int n) {
    switch(n) {
    case 1: 
      return 1;
    case 2:
      return 2;
    case 3:
      return 4;
    default:
      return doCalc(n - 1) + doCalc(n - 2) + doCalc(n - 3);
    }
  }

  public static void main(String[] args) {
    for(int i = 1; i <= 10; i++) {
      System.out.printf("f(%d) = %d\n", i, doCalc(i));
    }
  }
}