마방진의 정의는 다음과 같습니다.
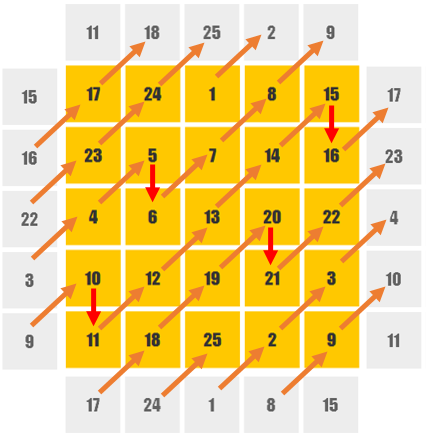
마방진(魔方陣)은 n2개의 수를 가로, 세로, 대각선 방향의 수를 더하면 모두 같은 값이 나오도록 n × n 행렬에 배열한 것이다. (…) n이 홀수일 때에는 마방진을 간단한 방법으로 만들 수 있다. 첫 번째 행의 가운데 칸에 1을 넣는다. 이어서 다음과 같은 규칙으로 숫자를 채운다. 다음 숫자를 대각선 방향으로 오른쪽 위 칸에 넣는다. 이때 해당하는 칸이 마방진의 위쪽으로 벗어난 경우에는 반대로 가장 아래쪽의 칸으로, 마방진의 오른쪽으로 벗어나는 경우는 가장 왼쪽의 칸으로 각자 한번 더 이동한다. 그리고 다른 수가 오른쪽 위 칸에 있어도 경우에 따라 수직 또는 수평으로 이동한다.
import blog.gui.PrintArray;
public class MagicSquare {
public static void main(String[] args) {
int[][] sq = new int[8][8];
int row = 1; // 첫 번째 행
int col = 3; // 세 번째 열
for (int n = 1; n <= 25; n++)
{
// 1행 3열에서 1부터 시작한다.
// row, col은 for문이 진행되면서 계속 변한다.
sq[row][col] = n;
// 행수는 하나 줄이고 열수는 하나 늘린다.
// 그것들을 nRow, nCol 이라 칭한다.
int nRow = row - 1;
int nCol = col + 1;
if(nRow == 0) nRow = 5;
// nRow가 만약 0이라면 5*5 영역 외 범위이므로
// 5행으로 바꿔준다.
if(nCol == 6) nCol = 1;
// nRow가 만약 6이라면 5*5 영역 외 범위이므로
// 1열로 바꿔준다.
if (sq[nRow][nCol] == 0)
{
row = nRow;
col = nCol;
}
// 대각선에 올라가봤더니 값이 0이라면 (비어 있다면)
// nRow와 nCol을 row, col에 대입시켜 다음 칸으로 이동한다.
// ↗ 방향이다.
else
row = row + 1;
// 대각선에 올라가봤더니 값이 0이 아니라면(비어있지 않다면)
// 이미 전에 n값이 기록된 칸이므로 (1, 6, 11 등 참고)
// ↓ 밑으로 이동한다.
}
new PrintArray(sq);
// 가로, 세로, 대각선의 합이 맞는지 검증
int rowSum = 0, colSum = 0, diagSum = 0;
for(int i = 0; i < sq.length; i++) {
for(int j = 0; j < sq.length; j++) {
if(i == 1) {
rowSum += sq[1][j]; // 가로 합
}
if (i == j) {
diagSum += sq[i][j]; // 대각선 합
}
}
colSum += sq[i][1]; // 세로 합
}
System.out.printf("%d, %d, %d", rowSum, colSum, diagSum);
}
}
그림을 따라가면서 보면 됩니다. 헷갈림을 방지하기 위해 [1][1] 에서 시작할 수 있도록 배열 크기를 충분히 크게 선언하였습니다. (원래 자바의 배열은 0부터 시작) new PrintArray()는 Java Swing 예제: 다차원 배열 표시하기 (기초 설정 방법, for문으로 swing 요소 반복 등) 에 있습니다.





0개의 댓글